Finite elements in the cloud

Pretend for a minute that you were one of the fellows up there posing for the picture back in the 1930s during the construction of the Waldorf Astoria in Manhattan. You would probably want to be sure that the engineers who designed the building had actually performed calculations of the beam you are standing on. Wouldn’t you?

Engineers have known how to solve beams with paper and pencil since the time of Galileo Galilei. The Euler-Bernoulli equations are easily found today on Wikipedia. But what about the hooks that the beam is hanging from? A curved beam with a non-uniform cross section? No, the answer is of course finite elements.

Engineers solve problems cost-effectively

An engineer is not someone who has a neat college degree or a fancy PhD diploma. An engineer is someone who solves problems. And builds things, and creates stuff from scratch. I do not buy that old saying that “engineering is applied science.” Sure, what’s not to love about knowing the difference between Newton’s and Lagrange’s formulations of classical mechanics? It is great to know how to go from the Peano axioms to Krylov subspaces. But we do not employ just science in our endeavors. We use expert judgment, we apply our past experience, we ask around for other people’s advice, and we bring to the table a lot of other tricks like ingenious out-of-the-box thinking.

This is actually what the etymology of the word “engineer” tells us. Our profession’s name does not come from engines, but the other way round: it comes from the Proto-Indo-European gene that means “to create” or “to invent,” which turned out first to ingeniare and then to ingenium in late Latin, which also means “device.” From there to ingenious thinking we have only a few steps, although other languages like the French ingénieur or my native Spanish ingeniero are closer to the original reference. In any case, not only do we have to solve problems, but also to obtain cost-effective solutions. That requires ingenium (and sometimes a little bit of genius, which is also part of the etymology).

Anyone can build “big” hooks and move on. But we engineers build just “big-enough” (and heavy-enough and costly-enough) hooks. We are constantly optimizing variables, especially time and cost. Unless we go the curved-non-uniform beam path we need a finite-elements tool to simulate (I would rather say to model) the stresses within the hook for the design loads. So let us fire our super-powerful and extremely-complex finite-element analysis program and see what happens, right? Well, there is still another engineering-friendly way.

Innovation & quantum potential barriers

Try to remember what came to your mind when you heard about Onshape for the first time and they said “CAD on the cloud.” I remember what I thought: “it cannot be done.” To my surprise, not only was it doable, but it turned out to be the best way to do CAD after all.

When we change our way of working we have to climb a “potential barrier” very much like a neutron before inducing fission of an uranium nuclei. It is hard to leave our comfort zone, because we spend most of our time there. But switching from desktop-based CAD to Onshape payed off afterward, didn’t it? (If you have not switched yet, trust me, it will pay off). But the path was not easy. You might have also had to drag people behind you because they did not want to leave their comfort zone.

Most of the time I feel like the caveman with the wheel in his hand. But I have to admit, sometimes I feel like the ones who stubbornly try to move the cart. What about you? And what about the leadership or your colleagues at your company?

Simple problems need simple solutions

Say you follow state-of-the-art engineering recommendations and design a crane hook online with Onshape. Now you wish to know how many tons the hook can withstand. Would you buy and install a complex and expensive piece of finite-element software plus all the required hardware? Why would you drag a simple hook down into such a magnificent beast’s jaws? That does not sound like engineer-likely, and certainly is neither time nor cost effective.

Surely, you would rather open a new tab and solve for the stresses in less than one minute:

Three simple steps (well, actually four)

Follow the following steps to quickly perform a finite-element analysis of an Onshape Part Studio. After completing the very first one, you will be able to go back and forth through the remaining three, which are the main steps of the CAEplex approach.

Step #0: Create case

After subscribing to CAEplex in Onshape’s App Store, open the document that contains the part studio you want to analyze. Click on the plus ‘+’ sign in the lower toolbar, go to “Add application…” and pick “CAEplex.” A new tab will be created, from which you can select the part studio and pick the problem type you want to solve: mechanical or thermal.

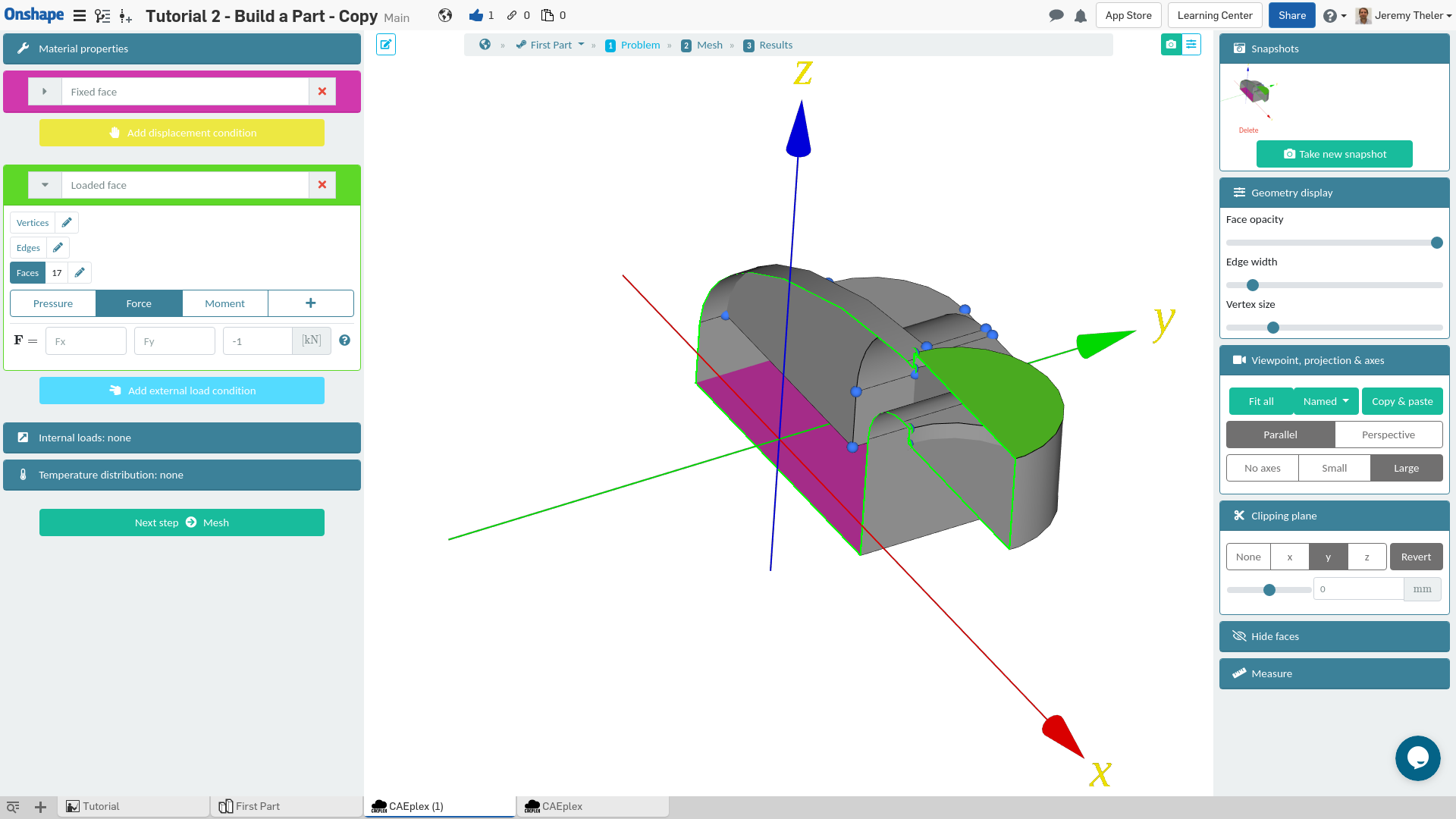
Step #1: Problem

Set the material properties and pick which faces (or edges or points) will have displacement conditions (i.e. fixed for instance) and the faces (or edges or points) that will have external loads conditions (e.g. a compression pressure). You can access hard-to-reach locations by clipping the geometry or by hiding surfaces with the toolbar from the right. You may include optional volumetric loads such as self-weight and/or a temperature distribution to take into account thermal expansion.

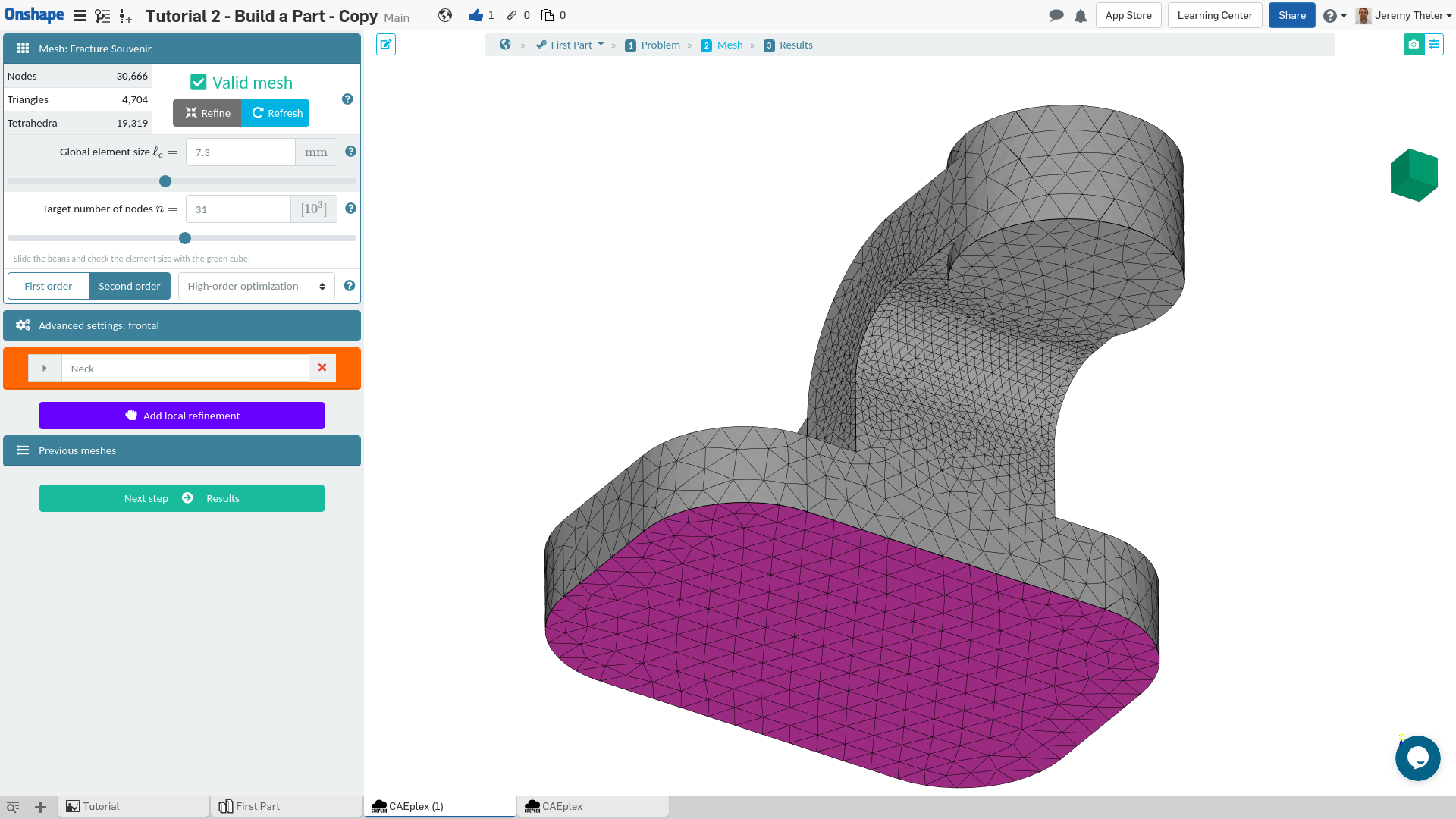
Step #2: Mesh

After completely defining the continuous problem, it is time to create a finite element mesh. Either first or second order tetrahedra can be generated using a few different 2D and 3D algorithms. You can locally refine around certain faces, edges or vertices. In the event that the mesher fails and a suitable grid cannot be generated, please contact our support staff with the chat button at the bottom-right corner. All meshing errors can be fixed by a suitable set of settings and/or by slight modifications of the original CAD geometry. Keep in mind that CAEplex aims at ease and speed. If you need to solve a many-solid problem with complex interfaces, you might be better off with the magnificent beast above. Or you can even use a tool that avoids meshing in the first place.

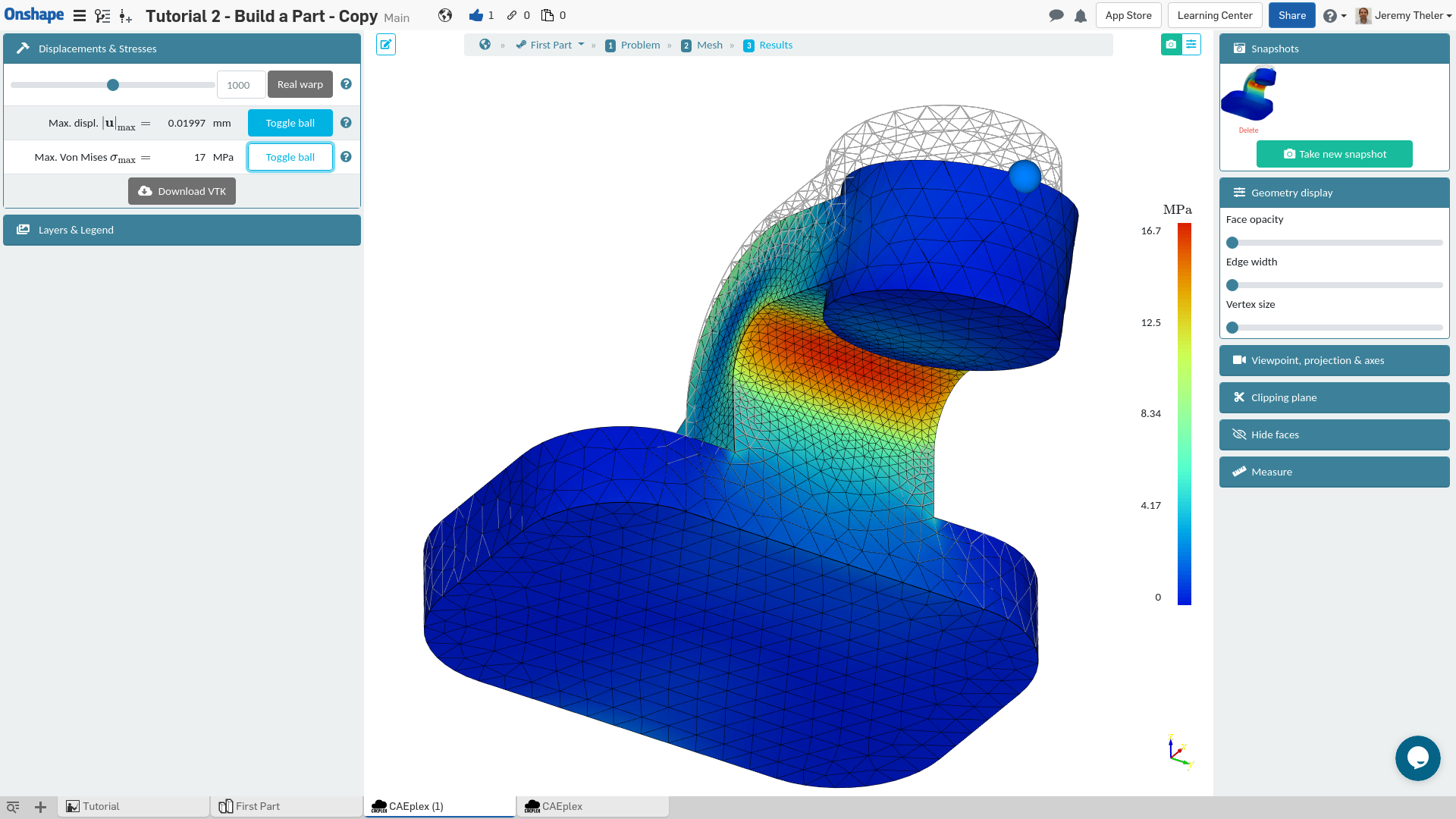
Step #3: Results

After CAEplex builds the stiffness matrix, solves the linear problem and computes the stresses out of the nodal displacements, step #3 shows a colored map of the resulting Von Mises stresses. Displacements can be lively warped by dragging the slider, thus checking that the loads had the correct sign and lead to the expected directions. A comparison of the warped grid with the original can also be shown. Besides Von Mises stresses, you can check Tresca and the three Principal stresses along with displacements as scalar fields. The scale can be changed interactively and a full VTK file can be downloaded for further post-processing with an offline tool such as ParaView or Mayavi.

Simple-yet-powerful: thermomechanical problems

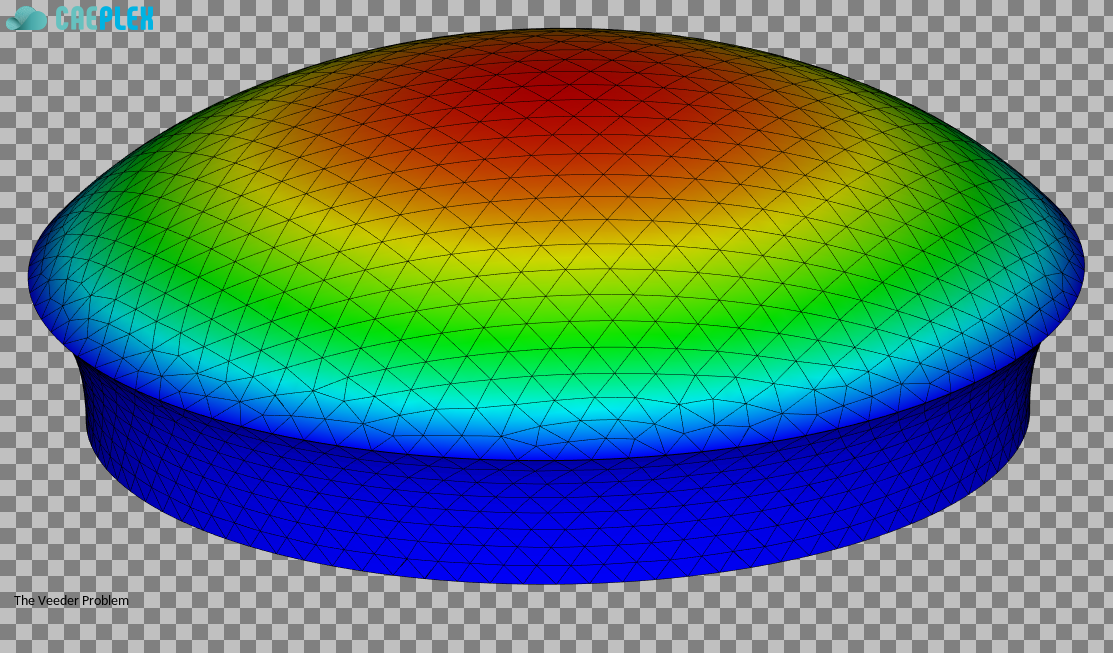
Let us now address thermoelastic expansion of finite cylinders by considering a simple cylinder of radius b standing on the x-y plane subject to the following temperature distribution

T(x,y,z) = T_0 \left(1 - \frac{x^2+y^2}{b^2}\right)

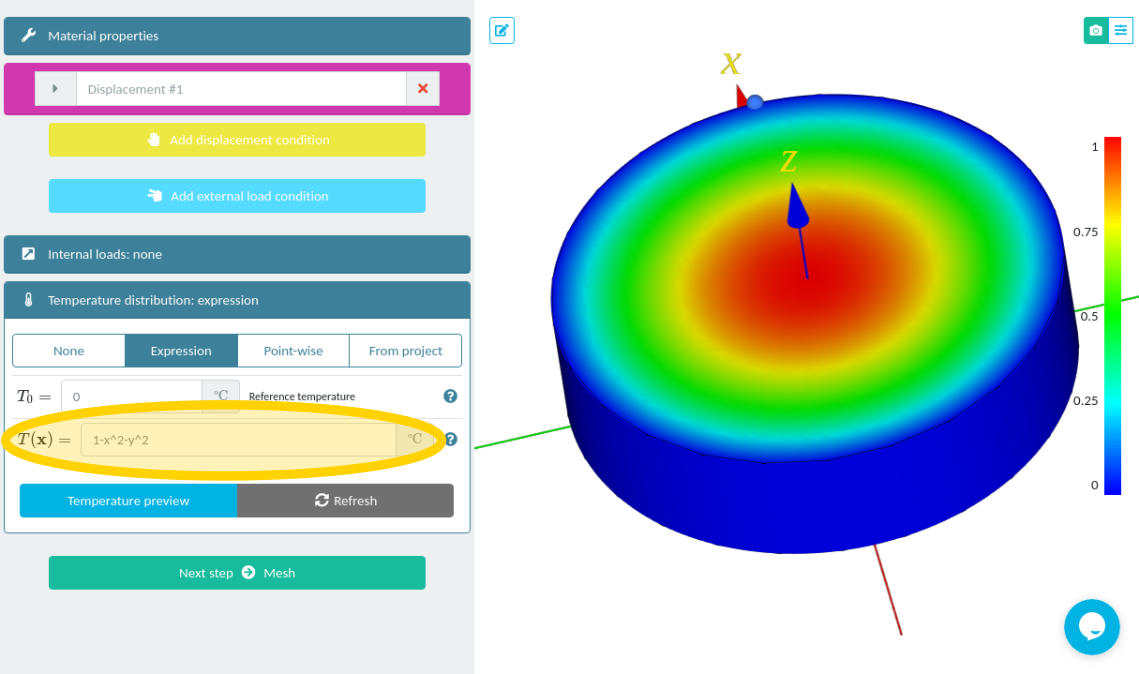
The question is: what are the displacements that this non-trivial temperature give rise to? The good news is that CAEplex has an algebraic parser: input boxes can handle not just regular numbers but also expressions like 1/2 instead of 0.5 or sqrt(pi/3) instead of square root of \pi/3. For b=1 mm the temperature can be simplified to 1-x^2-y^2, so that is what we write as T(\mathbf{x}):

After solving the problem, we can get a report or presentation-read image (i.e. with transparent-background):

What if we do not have an expression? CAEplex can interpolate 3D scattered data. But the best approach would be to perform the coupled thermal-mechanical computation, right? Well, yes but it is not a real “coupled” problem because (in the linear approach) the mechanical part does not influence the thermal problem. They are two linked problems.

So first we can solve thermal conduction to obtain the temperature distribution and then read it back from the mechanical problem. Instead of writing an algebraic expression, we pick the thermal project from the combo. Note that it is not needed to have the same mesh in both the mechanical and thermal cases, only the same geometry. Actually the thermal problem should use first order elements while the mechanical problem should use second order ones. Even more, local refinements should be performed at different locations. Traditional FEM programs usually do not allow this kind of flexibility.

New features and updates

All the benefits you get when using a 100% cloud-based product like Onshape (such as automatic updates and unmatched speed) also apply to CAEplex. This is possible due to a careful bottom-up design. Even more, the company behind CAEplex also developed the free and open source finite-element solver it uses from scratch. Therefore, Seamplex controls the full spectrum of the computation.

Our development team is continuously improving the product and adding new features, both to the interface and to the solver. Of course they will be automatically deployed to the cloud, but stay tuned for news because we will shortly release extensions like a report generator, parametric analysis of mesh convergence, computation of linearized ASME stresses, material libraries, etc. In any case, you can reach our support team with the chat button. We will be happy to discuss your modeling questions!